Измерения
Общее правило R для измерения (или наблюдения) требует, чтобы различные состояния квантовой системы, которые могут быть одновременно увеличены до классического уровня (на котором система должна выбрать одно из них), всегда должны быть взаимно ортогональны. Набор альтернатив, отобранный в результате полного измерения, образует систему ортогональных базисных векторов. Это означает, что каждый вектор в гильбертовом пространстве может быть (единственным образом) представлен в виде линейной комбинации этих векторов. Для измерения положения, произведенного над системой, состоящей из одной частицы, такие базисные векторы определяют те самые оси в конфигурационном пространстве состояний, о которых мы уже упоминали. Для измерения импульса это был бы другой набор, определяющий оси в импульсном пространстве состояний. Для полного измерения любого другого рода этот набор также был бы другим. После измерения состояние системы скачком переходит на одну из осей набора, соответствующего данному измерению, причем выбор оси происходит чисто случайным образом. Не существует динамического закона, который сказал бы нам, какая из осей будет выбрана природой. Ее выбор случаен, а значения вероятности определяются квадратами модулей амплитуд вероятности.
Предположим, что над системой, состояние которой |ψ), произведено некоторое полное измерение, причем базисом для выбранного измерения служит набор
|0), |1), |2), |3)….
Так как эти состояния образуют полный набор, то любой вектор состояния и, в частности, |ψ) можно представить в виде их линейной комбинации[150]
|ψ) = z0|0) + z1|1) + z2|2) + z3|3) +….
Геометрически коэффициенты z0, z1, z2 …. являются величинами ортогональных проекций вектора |ψ) на различные оси |0), |1), |2), |3)…. (рис. 6.22).
Рис. 6.22. Величины ортогональных проекций состояния |ψ) на оси |0), |1), |2)…. дают требуемые амплитуды z0, z1, z2 ….
Сразу возникает желание истолковать комплексные числа z0, z1, z2 … как искомые амплитуды вероятности, квадраты модулей которых давали бы различные вероятности того, что после измерения наша система будет находиться, соответственно, в состояниях |0), |1), |2), |3)…. Однако этого еще нельзя сделать, пока не определена «шкала» различных базисных векторов |0), |1), |2)…. Для этого мы должны оговорить, что в некотором смысле эти векторы являются единичными (т. е. имеют единичную длину), и, таким образом, они образуют так называемый ортонормированный базис (элементы которого попарно ортогональны и нормированы на единицу)[151]. Если вектор |ψ) также нормирован на единицу, то искомые амплитуды действительно станут коэффициентами z0, z1, z2 …, вектора |ψ), а вероятности, которые требуется найти, будут равны |z0|2, |z1|2, |z2|2….. Если |ψ) — не единичный вектор, то приведенные выше числа пропорциональны, соответственно, искомым амплитудам и вероятностям. Действительные амплитуды будут равны
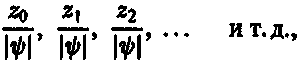
где |ψ) — «длина» вектора состояния |ψ).
Эта «длина» — положительное действительное число, определенное для каждого вектора состояния (0 имеет нулевую длину), и |ψ| = 1, если |ψ) — единичный вектор.
Полное измерение представляет собой весьма идеализированный тип измерения. Например, полное измерение положения частицы потребовало бы от нас способности локализовать частицу с бесконечной точностью, где бы во вселенной она ни находилась! К более элементарному типу измерения относится такое измерение, когда мы просто задаем вопрос типа «да или нет», например, такой: «Расположена ли частица справа (или слева) от некоторой прямой?» или «Лежит ли импульс частицы в некотором интервале?» и т. д. Измерения типа «да или нет» в действительности представляют собой наиболее фундаментальный тип измерения. (Например, используя только лишь измерения типа «да или нет», можно сколь угодно близко подойти к точному значению положения или импульса частицы.) Предположим, что результатом измерения типа «да или нет» оказывается ДА. Тогда вектор состояния должен находиться в области «ДА» гильбертова пространства, которую я обозначу Y (от англ. yes — «да». — Прим. ред.). С другой стороны, если результатом измерения типа «да или нет» оказывается НЕТ, то вектор состояния должен находиться в области «НЕТ» гильбертова пространства, которую я обозначу N (от англ. no — «нет». — Прим. ред.). Области Y и N полностью ортогональны друг другу в том смысле, что любой вектор состояния из области Y должен быть ортогонален любому вектору состояния из области N (и наоборот). Кроме того, любой вектор состояния |ψ) может быть (единственным образом) представлен в виде суммы векторов, принадлежащих каждой из областей Y и N. Если воспользоваться математической терминологией, то можно сказать, что области Y и N являются ортогональными дополнениями друг друга. Таким образом, |ψ) однозначно представи́м в виде
|ψ) = |ψY) + |ψN)
где |ψY) принадлежит Y, a |ψN) принадлежит N. Здесь |ψY) означает ортогональную проекцию состояния |ψ) на Y, a |ψN) — ортогональную проекцию состояния |ψ) на N (рис. 6.23).
Рис. 6.23. Редукция вектора-состояния. Измерение может быть описано в терминах пары подпространств Y и N, каждое из которых является ортогональным дополнением другого. После измерения состояние |ψ) скачком переходит в свою проекцию на одно из этих подпространств с вероятностью, задаваемой множителем, показывающим, во сколько раз квадрат длины вектора состояния уменьшается при переходе к проекции
Если результат измерения есть ДА, то |ψ) скачком переходит в |ψY), а если результат есть НЕТ, то в |ψN). Если вектор состояния |ψ) нормирован, то соответствующие вероятности того и другого исхода равны квадратам длин
|ψY|2 и |ψN|2 состояний-проекций. Если же вектор |ψ) не нормирован, то каждый из этих квадратов необходимо разделить на |ψ|2. (По «теореме Пифагора»